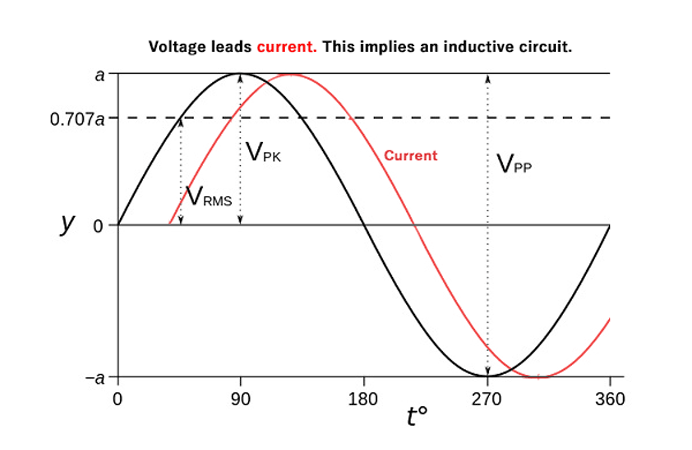
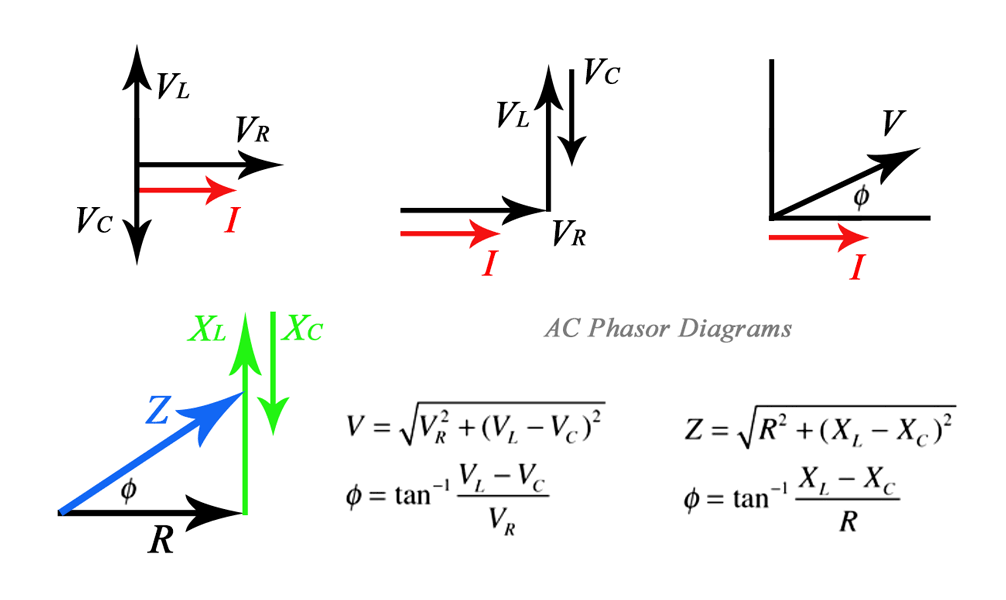When capacitors or inductors are found in an AC circuit, the associated current and voltage sine waves do not peak at the same time. The resulting difference between these offset peaks, expressed in degrees, is said to be the phase difference.
In alternating current theory, the phase difference is equal to or less-than 90 degrees. Typically the angle by which the voltage leads the current is used.
This leads to a positive phase for inductive circuits since current lags the voltage in an inductive circuit.
The phase is negative for a capacitive circuit since the current leads the voltage.
Phasor Diagrams
It can be easier to understand phase when defined as a vector in a plane. The usual reference for zero phase is taken to be the positive x-axis and is associated with the resistor since the voltage and current associated with the resistor are in phase.
The length of the phasor is proportional to the magnitude of the quantity represented, and its angle represents its phase relative to that of the current through the resistor. The difference in phase between the voltage and the current in an AC circuit, is the phase angle associated with the impedance (Z) of the circuit.
ELI the ICE man
The useful mnemonic ELI the ICE man helps to remember the sign of the phase. The phase relation is often depicted graphically in a phasor diagram.
ELI: Voltage leads current in an inductor. E (Voltage) L (Inductor) I (Current)
When voltage is applied to an inductor, it resists change in current. The current builds up more slowly than the voltage, lagging in time and phase.
ICE: Current leads voltage in a capacitor. I (Current) C (Capacitor) E (Voltage)
Since the voltage on a capacitor is directly proportional to the charge on it, the current must lead the voltage in time and phase to conduct charge to the capacitor plates and raise the voltage.