The laws of electricity describe the behavior of electrical charges, how they interact with each other, and how they produce electric fields and currents. These rules play a crucial role in shaping our understanding and use of electricity, from basic electrical circuits to advanced power systems.
The general laws that govern electricity are few and simple, but they are applied in an unlimited number of ways. By understanding the principles of electrical theory, engineers and technicians can design and optimize electrical systems and devices, ensuring that they are safe, reliable, and efficient.
Contents
- Ohm’s Law
- Watt’s Law
- Kirchhoff’s Current Law (KCL)
- Kirchhoff’s Voltage Law (KVL)
- Faraday’s Law
- Lenz’s Law
- Coulomb’s law
- Gauss’s Law
- Conventional Current vs. Electron Current
- Right Hand Rules
- ELI the ICE Man
Ohm’s Law
The current through a conductor between two points is directly proportional to the voltage across the two points.
I = V / R or V = IR or R = V/I
Where I is the current through the conductor in units of amperes, V is the voltage measured across the conductor in units of volts, and R is the resistance of the conductor in units of ohms. More specifically, Ohm’s law states that the R in this relation is constant, independent of the current.
1 Ohm = resistance of a conductor when a potential difference of one volt produces a current of one amp through the conductor.
Watt’s Law
Similar to Ohm’s law, Watt’s law states the relationship between power (watts), current and voltage.
P = VI or P = I2R
Related: Ohm’s Law & Watt’s Law Calculator
Kirchhoff’s Current Law (KCL)
The total current or charge entering a junction or node is exactly equal to the charge leaving the node as it has no other place to go except to leave, as no charge is lost within the node. In other words, the algebraic sum of ALL the currents entering and leaving a node must be equal to zero.
Current In = Current Out
Further Reading: Divider Circuits And Kirchhoff’s Laws
Kirchhoff’s Voltage Law (KVL)
In any closed loop network, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop, which is also equal to zero. In other words, the algebraic sum of all voltages within the loop must be equal to zero.
Further Reading: Divider Circuits And Kirchhoff’s Laws
Faraday’s Law
The induced electromotive force in any closed circuit is equal to the negative of the time rate of change of the magnetic flux enclosed by the circuit.
E=dB/dt
(Electromotive Force = change in magnetic flux / change in time)
Simply put, the bigger the change you have in the magnetic field, the greater amount of voltage. This law explains the working principle of most electrical motors, generators, electrical transformers and inductors.
Further Reading: Faraday Law of Electromagnetic Induction
Lenz’s Law
The direction of current induced in a conductor by a changing magnetic field due to Faraday’s law of induction will be such that it will create a magnetic field that opposes the change that produced it. Simply put, the magnitude of the emf induced in the circuit is proportional to the rate of change of flux.
Further Reading: Lenz Law of Electromagnetic Induction
Coulomb’s law
The magnitude of the electrostatic force of attraction between two point charges is directly proportional to the product of the magnitudes of charges and inversely proportional to the square of the distance between them.
The force is along the straight line joining them. If the two charges have the same sign, the electrostatic force between them is repulsive; if they have different signs, the force between them is attractive.
F = k q1 q2 / r2
F is the resulting force between the two charges. The distance between the two charges, or radius of separation is r. The q1 and q2 values represent the amount of charge in each of the particles. The constant of the equation is k.
Further Reading: Electric Force and Coulomb’s Law
Gauss’s Law
The total of the electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. The electric flux through an area is defined as the electric field multiplied by the area of the surface projected in a plane perpendicular to the field.
The integral form of Gauss’ Law finds application in calculating electric fields around charged objects. Gauss’ law is a powerful tool for the calculation of electric fields when they originate from charge distributions of sufficient symmetry to apply it.
Further Reading: Gauss’s Law and Electric Flux
Conventional Current vs. Electron Current
Conventional Current assumes that current flows out of the positive terminal, through the circuit and into the negative terminal (+ > -) of the source. This was the convention chosen during the discovery of electricity.
We now know this is incorrect. In conductors, the charge carrier is the electron whose charge is negative.
The flow of electrons is termed electron current. Electrons flow out of the negative terminal, through the circuit and into the positive terminal of the source (+ < -).
In reality, it makes no difference which way current is flowing as long as it is used consistently. The direction of current flow does not affect what the current does.
Further Reading: Conventional Current vs Electron Flow
Right Hand Rules
Rule #1 determines the directions of magnetic force, conventional current and the magnetic field. Given any two of theses, the third can be found.
- Using your right-hand: point your index finger in the direction of the charge’s velocity (recall conventional current).
- Point your middle finger in the direction of the magnetic field.
- Your thumb now points in the direction of the magnetic force.
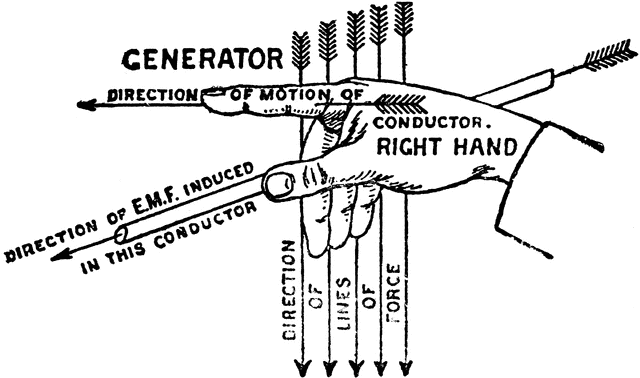
Electrical Theory Fundamentals Right Hand Rules.
Rule #2 determines the direction of the magnetic field around a current-carrying wire and vice-versa.
- Using your right-hand: Curl your fingers into a half-circle around the wire, they point in the direction of the magnetic field.
- Point your thumb in the direction of the conventional current.
Further Reading: Right-Hand Rules: A Guide to finding the Direction of the Magnetic Force
ELI the ICE Man
When capacitors or inductors are involved in an AC circuit, the current and voltage do not peak at the same time. The fraction of a period difference between the peaks expressed in degrees is said to be the phase difference.
ELI
Voltage leads current in an inductor. E (Voltage) L (Inductor) I (Current)
When voltage is applied to an inductor, it resists change in current. The current builds up more slowly than the voltage, lagging in time and phase.
ICE
Current leads voltage in a capacitor. I (Current) C (Capacitor) E (Voltage)
Since the voltage on a capacitor is directly proportional to the charge on it, the current must lead the voltage in time and phase to conduct charge to the capacitor plates and raise the voltage. The phase difference in each case is equal to or less than 90 degrees.
Further Reading: Phase and Phasor Diagrams
